新奇な超伝導とその発現機構
超伝導とはある物質が特定の温度以下で電気抵抗をゼロにする現象です。通常の金属では、温度を下げると抵抗が減りますが、超伝導体は完全に電気抵抗が消えます。これにより、エネルギー損失がなく、永久に電流の流れが可能になります。
銅酸化物高温超伝導体
銅酸化物高温超伝導体は、液体窒素温度付近でも超伝導性を示し、未解明のメカニズムが魅力です。特に、非磁性のCDW相が超伝導相のど真ん中に発見され、CDWが超伝導にどのように寄与するのかは重要な課題です。CDW相と超伝導、疑ギャップとの関係が超伝導の理解に必要なカギとなります。これらの複雑な相互作用は、平均場近似では説明できず、高次の多体相関を扱う手法が不可欠です。
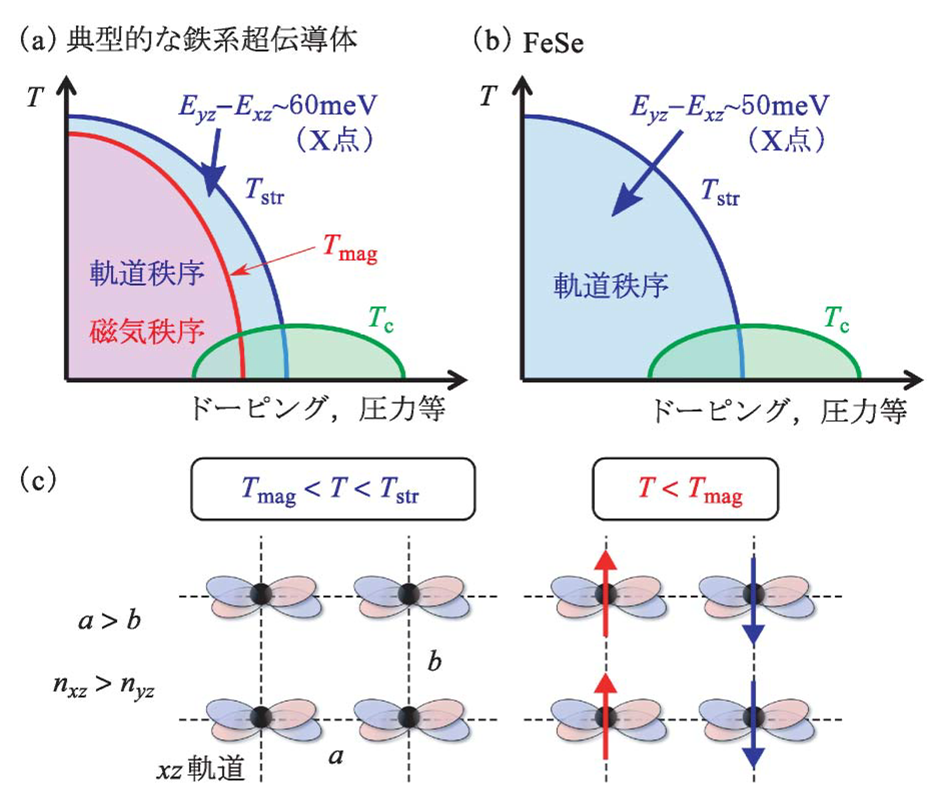
鉄系超伝導体
鉄系超伝導体は、高温で超伝導を示す一方で、ネマティック相やスピン密度波（SDW）などの異常相を持ちます。特に、FeSe系のように磁気秩序が見られない材料で、ネマティック相が超伝導の前駆相として現れることが注目されています。このネマティック相が超伝導に与える影響を解明することが、超伝導メカニズムの理解に重要です。こちらも、平均場近似では捉えきれない相互作用を扱うため、高次の多体計算が求められます。
カゴメ格子金属の多重量子相
カゴメ格子超伝導体
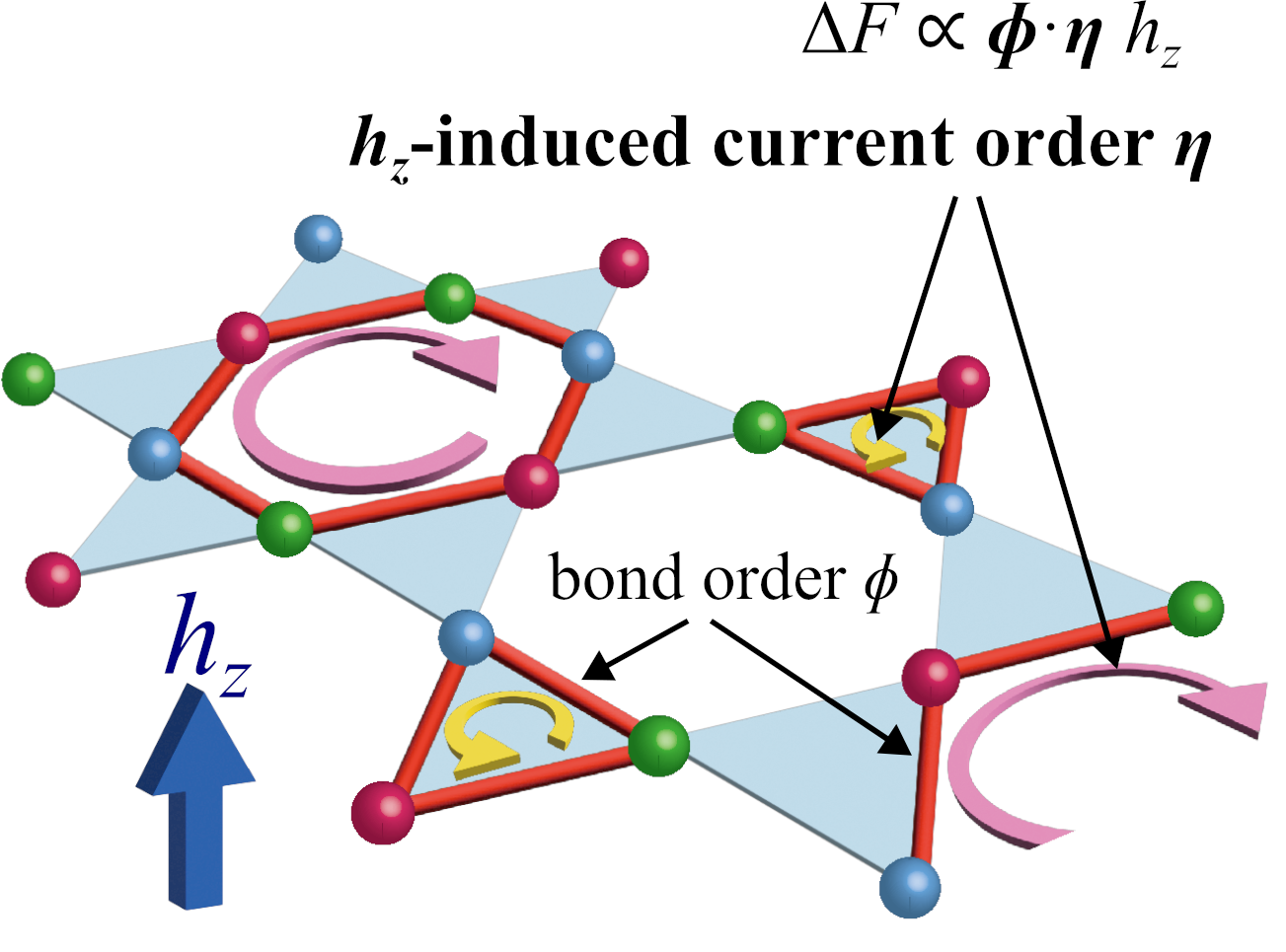
カゴメ格子は2次元のフラストレーション系で、従来はスピン磁性が議論の対象でした。ところが2019年から相次いで発見されたCsV₃Sb₅などのカゴメ格子超伝導体は、様々な興味深い量子相が実現する舞台として、近年非常に注目されています。CDW相（密度波相）と超伝導相が共存し、さらにループ電流秩序が時間反転対称性を破る新しい現象が確認されています。通常、超伝導体は時間反転対称性を保ちますが、この秩序では非スピン分極の時間反転対称性が破れ、従来の超伝導体にはない特徴を示します。
このループ電流に起因する時間反転対称性の破れは、波動関数の位相空間上の距離に相当する量子計量と協力して、巨大非相反応答などの興味深い副産物を生み出し、新しい物理的現象が観察されます。例えば、非相反応答は新たな量子デバイスやエネルギー技術に応用される可能性があります。カゴメ格子金属は、トポロジカル相や新しい量子相の発見にもつながり、物性研究における重となる可能性があります。
強相関多体系の計算手法
バーテックス補正とその効果
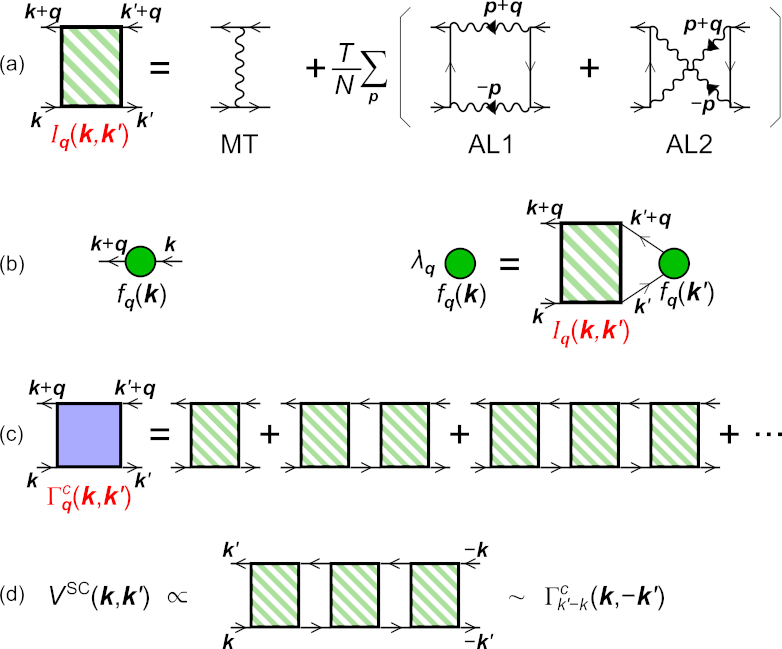
従来の手法（例えば、平均場、RPA、FLEXなど）は、磁気揺らぎは議論できますが、電荷チャンネルの揺らぎを十分に扱うことができません。しかし、バーテックス補正を導入することで、電荷チャンネルの揺らぎ発達、さらに非局所的な相互作用が導かれます。この補正により、ボンド秩序や電流秩序といった新奇な非局所秩序の説明が可能となります。特に、Aslamazov – Larkin項として知られる揺らぎ間の干渉機構は、鉄系超伝導体のネマティック秩序や銅酸化物のCDW、カゴメ格子のCDWといった非磁性秩序を自然に説明します。
繰り込み群法の改良
また、汎関数繰り込み群法（RG法）の改良も重要な貢献です。特に、フェルミ面上を細かく分割し、2次元電子系に対する繰り込み群法を解く手法は、相互作用を精緻に捉える強力な手法です。さらに、制限RPA法との組み合わせにより、繰り込み群法が苦手な高エネルギー領域も組み込むことが可能になりました。本手法は高精度ですが結果の物理的な起源を見出すのが難しく、バーテックス補正による摂動計算と相補的です。
高精度計算手法の開発
さらに、基礎的な計算の高精度化も行っていますFLEX近似を極低温で適用するために、波数・振動数依存性を圧縮した計算手法も開発しました。低エネルギーから高エネルギーまで波数メッシュを段階的に削減させ、従来の約100倍の振動数を効率よく計算することができます。
トポロジカル物質、新規超伝導体、熱電材料の共同研究
CaAgAs、CaAgPの研究
これらの物質に着目したのは、東京大学の岡本先生（当時名古屋大学所属）です。第一原理計算のデータベースを参考に、当初はバンド分散が線形に交差するディラック電子系と予測されていました。ところが私が第一原理計算を行った結果、線形分散が点ではなくリング状に繋がった非常にユニークなバンド構造を持つち、現在ではノーダルライン系と呼ばれている（当時はほぼ知られていなかった）物質であることがわかりました。さらに、スピン軌道相互作用を考慮するとギャップが開くため、私が第一原理計算から強束縛模型を構築、名古屋大学の山影さんがトポロジカル絶縁体の性質を議論しました。この物質の特筆すべき点は、ノーダルラインがフェルミ準位にあり、他のバンドが近傍に存在しないことです。また、実験的にも空気中で安定な非常に貴重な系であり、岡本先生が実際に物質合成と物性測定を行いました。
１次元トポロジカル物質における高い熱電特性
Ta₄SiTe₄は非常に1次元的でディラック的なバンド分散を持ち、高い熱電特性を示すことが分かりました。私の貢献は、第一原理計算に基づいてバンド構造を解析し、その特性を明らかにすることでした。
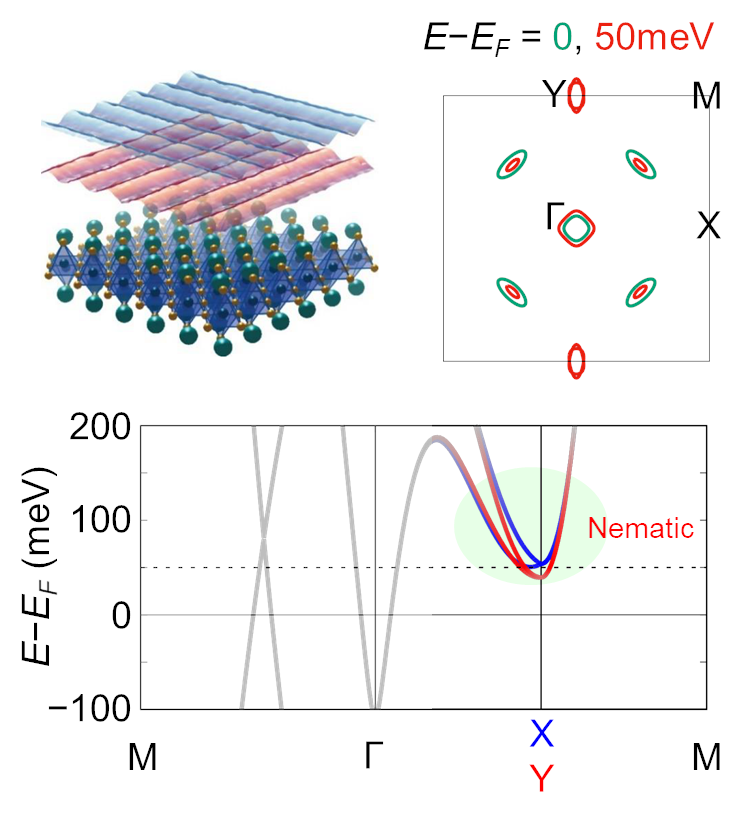
ディラック電子系BaNiS₂のネマティック
理研の花栗グループとの共同研究です。BaNiS₂がディラック分散を持つ物質ですが、花栗グループのSTM測定から、電子系が回転対称性を破り電子ネマティック液晶状態になることが発見されました。不思議な事に、この異方性はエネルギー依存性を持ち、フェルミ準位近傍ではなく高エネルギー領域のバンドで顕著に観測されました。私の理論的貢献は、バーテックス補正を考慮した多体電子計算を用いて、ボンド秩序による異方的電子液晶化の発生メカニズムを明らかにし、STM測定結果と整合したバンド分散を得ました。
using WordPress and